En un sistema de coordenadas cartesianas x-y, la circunferencia con centro en el punto (a, b) y radio r consta de todos los puntos (x, y) que satisfacen la ecuación
 .
.
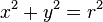 .
.
De la ecuación general de una circunferencia,
 ,
,la ecuación de la circunferencia es:
Ecuación vectorial de la circunferencia
La circunferencia con centro en el origen y radio R, tiene por ecuación vectorial:  Donde teta es el parámetro de la curva, además cabe destacar que
Donde teta es el parámetro de la curva, además cabe destacar que  Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.
Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.
 Donde teta es el parámetro de la curva, además cabe destacar que
Donde teta es el parámetro de la curva, además cabe destacar que  Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.
Se puede deducir fácilmente desde la ecuación cartesiana, ya que la componente X y la componente Y, al cuadrado y sumadas deben dar por resultado el radio de la circunferencia al cuadrado. En el espacio esta misma ecuación da como resultado un cilindro, dejando el parámetro Z libre.Ecuación en coordenadas polares
Cuando la circunferencia tiene centro en el origen y el radio es c, se describe en coordenadas polares como 
 y el radio es
y el radio es  , la ecuación se transforma en:
, la ecuación se transforma en:

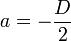






![x=a + c \cos t,\ y=b+c\sin t,\qquad t\in[0,2\pi]](http://upload.wikimedia.org/wikipedia/es/math/f/d/0/fd08b31a7dac369664c95f143fb10657.png)

No hay comentarios:
Publicar un comentario